

 Back Back |
 Table
of contents Table
of contents |
 Next Next |

Minimum spanning trees
In this section we first describe an algorithm which solves
a more general task. That is to find, given a weighted, connected and undirected
graph, a spanning-tree of minimum weight. This problem may appear in a
number of guises, the most common of which concerns the construction of
a communivation network, perhaps a road or a railway system linking
a set of towns, the problem is to find a network at minimum cost and which
provides some route between every two towns.The solution is minimum-weight
spanning-tree of the associated complete weighted graph.Because of this
description , the problem is often called the connector problem.
There are a number of algorithms known to solve
the connector problem for undirected graphs. The best known of these
are due to Prim and to Krukal. Each can be made to run in time O(E lg V)
using binary heaps.
Growing a minimum spanning tree
The greedy strategy is captured
by the following "generic" algorithm, which grows the minimum spanning
tree one edge at a time. The algorithm manages a set A which is always
a subset of some minimum spannning tree. At each step, an edge (u,v)
is determined that can be added to A without violating this invariant,
in the sense that A U { (u, v) } is also a subset of a minimum
spanning tree. We call such an edge a safe edge for A.
GENERIC-MST(G,w)
1 A <- empty
Some
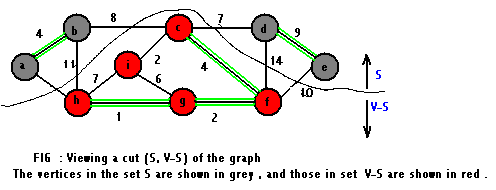
definitions: A cut (S,V-S) of an undirected graph G
= (V, E) is a partition of V(shown in the figure).We say
that an edge (u, v) belonging to E crosses tha cut (S,
V-S) if one of its endpoints is in S and the other is in V-S.
We say that a cut respects the set a of edges if no edge in A crosses
the cut. An edge is a light edge crossing the cut if its weight is the
minimum of any edge crossing the cut.
Theorem: Let G = (V, E)
be a connected, undirected graph with a real valued weight function defined
on E. Let A be a subset of E that is included in some
minimum spanning tree for G, let (S, V-S) be any cut of G
that respects A, and let (u, v) be alight edge crossing (S,
V-S). Then, edge (u, v) is safe for A.
Proof: Refer Cormen
A spanning-tree of a connected undirected graph G
is a subgraph which is both a tree and which contains all the vertices
of G.Such a spanning tree can be found in linear-time using, for example
, a depth-first search.
The two algorithms also illustrate a heuristic for optimization
called the "greedy" strategy. At each step of the algorithm, one of the
several possible choices must be made. The greedy method advocates making
the choice that is best at the moment. Such a strategy is not guaranteed
to find optimal solutions to problems. For the minimum-spanning tree problem,
however, we can prove that this does yield a minimum spanning tree.
2 while A
does not form a spanning tree
3
do find an edge (u, v) that is safe for A
4
A <- A U { (u, v) }
5 return A