 Back |
 Table
of contents |
 Next |
Elementary graph algorithms
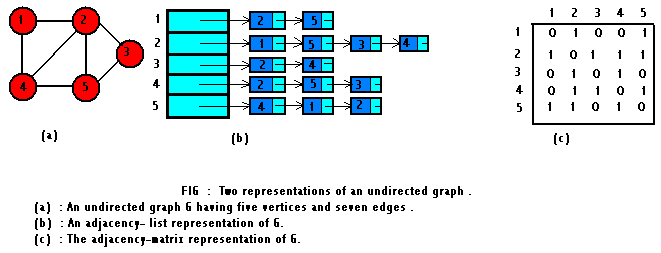
The adjacency list representation of a graph G=(V,E)
consists of an array Adj of |V| lists, one for each vertex in V. For each
u belonging to V, the adjacency list Adj[u] contains pointers to all vertices
v such that there is an edge (u,v) belonging to E. That is, Adj[u] consists
of all the vertices adjacent to u in G.
Adjacency lists can be adapted to represent weighted graphs
,that is , graphs for which each edge has an associated weight
, typically given by a weight function
w : E ->R .For example ,let G = (V,E) be a weight
graph with weight function w.The weight w(u,v) of the
edge
(u,v) belonging to E is simply stored with vertex v in
u's adjacency list..
For the adjacency-matrix representation of a graph
G = (V,E) , we assume that the vertices are numbered 1,2,..... |V| in some
arbitrary manner . The adjacency-matrix representation of a
graph G then consists of a |V|*|V| matrix A= (aij)
such
that
Like the adjacency list representation adjacency matrix representation
can be used for weighted graphs .The weight w(u,v)of
the edge (u,v) can be stored as the entry in row
u and colomn v of the adjacency matrix
.If an edge does not exist , a NIL value can be stored as its corresponding
matrix entry .
Although the adjacency-list representation is asymptotically
at least as efficient as the adjacency-matrix representation
, the simplicity of the latter may make it preferable when graphs
are reasonably small . Moreover ,if the graph is unweighted ,there is an
additional advantage in storage for the adjacency-matrix representation.
Rather than using one word of computer memory for each matrix entry ,it
uses only one bit per entry.
This chapter presents methods for representing a
graph and for searching a graph. Searching a graph means systematically
following the edges of the graph so as to visit the vertices of the graph.
Techniques for searching a graph are at the heart of the field of graph
algorithms.
Representations of Graphs
There are two standard ways to represent a graph G=(V,E):
as a collection of adjacency lists or as an adjacency matrix. The adjacency
list representation is usually prefered, because it provides a compact
way to represent sparse graphs-those for which |E| is much less than |V|2.
aij = { 1 if (i,j) belongs
to E
0 otherwise .